立体视觉计算视差图 stereo vision

一、实验原理

1、立体图像

立体视差也就是立体视像，是基于双眼视差所获得的深度知觉。所谓立体图像，其实就是有两台水平的相机对同一场景进行观测，这时，得到的两幅图像就有了相同的图像平面，图像的行是对齐的。
参考图如下所示：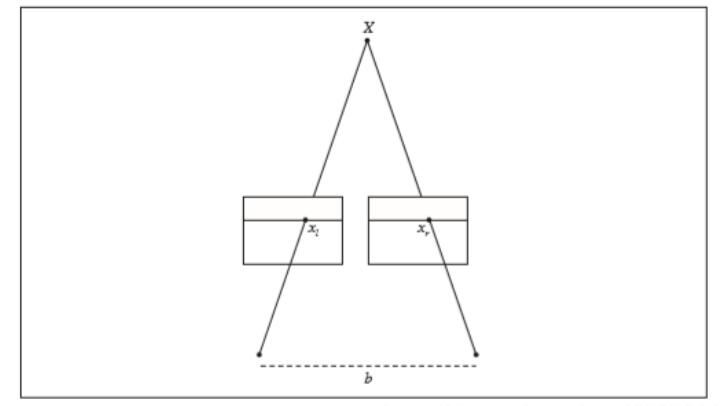

由于采用的图像是官网提供的图片，是已经矫正过的，所以这两幅图就可以看成是理想的。根据偏移可以计算出深度，公式如下：

$Z=\frac{fb}{x_l-x_r}$

其中，$f$是焦距，$b$是两个相机中心的距离，$x_l$和$x_r$分别是左右两个图像中的$x$坐标，分开照相机中心的距离成为基线。

2、计算视差

在立体重建算法中，对图像中的每个像素尝试不同的偏移，并按照局部图像周围归一化的互相关值，选择具有最好分数的偏移，记录该最佳偏移。

3、归一化互相关NCC

归一化互相关算法原理为：对于已经矫正过的两个图像$I_1$和$I_2$，ncc算法对图像$I_1$一个待匹配像素构建一个匹配窗口，在另一个图像的极线上对每个像素构建匹配窗口与待匹配像素匹配窗口计算相关性，相关性越高则表示匹配度越好。

下面对每个像素周围的像素块来计算归一化相关值，公式如下：

$ncc(I_1,I_2)=\frac{\Sigma_x(I_1(X)-\mu_1)(I_2(X)-\mu_2)}{\sqrt{\Sigma_x(I_1(X)-\mu_1)^2}\sqrt{\Sigma_x(I_2(X)-\mu_2)^2}}$

二、实验步骤

得到计算视差图的基本步骤如下：

校正：校正的目的是为了使得两帧图像的光心处于同一水平线上，便于后续的ncc操作。
特征匹配：利用ncc做匹配，右视图中与左视图待测像素同一水平线上相关性最高即为最优匹配，完成匹配后，需要记录视差d，即待测像素水平方向$x_l$和匹配像素水平方向$x_r$之间的差值，再由上述推导的深度公式计算出深度$Z$，最终可以得到一个与原始图像尺寸相同的视差图。
由于不用窗口值会影响得到的视差图的效果，因此在不同窗口下对图像视差图进行求取，以此得到多个视差图。

三、实验代码

from scipy.ndimage import filters
import stereo
from PIL import Image
from scipy import misc
from scipy.ndimage import filters
from pylab import *
import numpy as np
import matplotlib.pyplot  as plt
# 定义归一化ncc方法
def plane_sweep_ncc(iml, imr, start, steps, wid):
    # 使用归一化的互相关计算视差图像
    (m, n) = iml.shape
    print(iml.shape)
    meanl = zeros((m, n))
    meanr = zeros((m, n))
    # meanl = zeros_like(iml)
    # meanr = zeros_like(imr)
    s = np.zeros((m, n))
    s_l = np.zeros((m, n))
    s_r = np.zeros((m, n))
    # 保存深度平面的数据
    deepmaps = np.zeros((m, n, steps))
    # 计算图像的平均值
    filters.uniform_filter(iml, wid, meanl)
    filters.uniform_filter(imr, wid, meanr)
    # 图像归一化处理
    norml = iml - meanl
    normr = imr - meanr
    # 计算不同视差
    for disp in range(steps):
        # 将左边图像加到右边的图像上
        filters.uniform_filter(np.roll(norml, -disp - start) * normr, wid, s)
        filters.uniform_filter(np.roll(norml, -disp - start) * np.roll(norml, -disp - start), wid, s_l)
        # 和反归一化
        filters.uniform_filter(normr * normr, wid, s_r)
        # 保存ncc的值
        deepmaps[:, :, disp] = s / sqrt(s_l * s_r)
    # 为每个像素选取最佳深度
    return argmax(deepmaps, axis=2)
# 高斯滤波器
def plane_sweep_guess(iml, imr, start, steps, wid):
    # 使用高斯的互相关计算视差图像
    (m, n) = iml.shape
#     print(iml.shape)
    meanl = zeros((m, n))
    meanr = zeros((m, n))
    # meanl = zeros_like(iml)
    # meanr = zeros_like(imr)
    s = np.zeros((m, n))
    s_l = np.zeros((m, n))
    s_r = np.zeros((m, n))
    # 保存深度平面的数据
    deepmaps = np.zeros((m, n, steps))
    # 计算图像的平均值
    filters.gaussian_filter(iml, wid, 0, meanl)
    filters.gaussian_filter(imr, wid, 0, meanr)
    # 图像归一化处理
    norml = iml - meanl
    normr = imr - meanr
    # 计算不同视差
    for disp in range(steps):
        # 将左边图像加到右边的图像上
        filters.gaussian_filter(np.roll(norml, -disp - start) * normr, wid, 0, s)
        filters.gaussian_filter(np.roll(norml, -disp - start) * np.roll(norml, -disp - start), wid, 0, s_l)
        # 和反归一化
        filters.gaussian_filter(normr * normr, wid, 0, s_r)
        # 保存ncc的值
        deepmaps[:, :, disp] = s / sqrt(s_l * s_r)
    # 为每个像素选取最佳深度
    return argmax(deepmaps, axis=2)
iml = np.array(Image.open('../input/stereo-sample/im0.png').convert('L'), 'f')
imr = np.array(Image.open('../input/stereo-sample/im1.png').convert('L'), 'f')
# 开始偏移并设置步长
steps = 50
start = 4
# ncc的宽度
wid = 30
for i in range(1, wid):
    # ncc方法
    # res_ncc = plane_sweep_ncc(iml, imr, start, steps, i)
    # 高斯方法
    print('宽度{}时的滤波结果！'.format(i))
    res_gaussian = plane_sweep_guess(iml, imr, start, steps, i)
    # imsave(r'.vscode\prml-myself\vision_ncc_out\{}.jpg'.format(i), res_ncc)
    imsave(r'./{}.jpg'.format(i), res_gaussian)

四、实验展示

原始图像如下：

对不同窗口下的视差图如下（窗口值从1-30,50，100）

窗口width	ncc方法	gaussian
1	1.jpg](https://i.loli.net/2021/10/23/1pf6BJWuRZSnLTV.jpg) \| ![1.jpg
5	5.jpg](https://i.loli.net/2021/10/23/PglouKOMWNjGkDp.jpg) \| ![5.jpg
30	29.jpg](https://i.loli.net/2021/10/23/GpSYfN156xAe23u.jpg) \| ![29.jpg
50	50.jpg](https://i.loli.net/2021/10/23/eKY8JXnmjfy1aEw.jpg) \| ![50.jpg
100	100.jpg](https://i.loli.net/2021/10/23/j9kLR4YpTyPvmMJ.jpg) \| ![100.jpg