LDA线性判别分析

基本概念

线性分类： 指存在一个线性方程可以把待分类样本分离开，或者用一个超平面将正负样本分开，表达式为

所谓超平面即是区分样本点的一个决策面，在二维世界中，可以理解为一条直线，如一次函数。
非线性分类： 指不存在一个线性分类能将样本分隔开，可以是一个曲面，也可以是多个超平面的组合。

LDA思想

核心思想：类内小，类间大
线性判别分析（Linear Discrimination Analysis, LDA）是一种监督学习的线性降维方法，即每个样本都是由类别的输出。其主要思想是”投影后类内方差最小，类间方差最大“，我们知道，对于一组数据来说，均值决定了它的中心，方差则是决定了这组数据的离散程度，越大越离散，越小越集中。在二分类问题中，我们将样本点在低纬度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，两种类别的数据点的中心尽可能的远离。

LDA算法的推导以及优化

LDA原理，投影到低纬度上的空间中，使得投影后的点会形成按类别区分一簇一簇的分布情况，相同类别的点较为集中，不用类别的点相聚较远。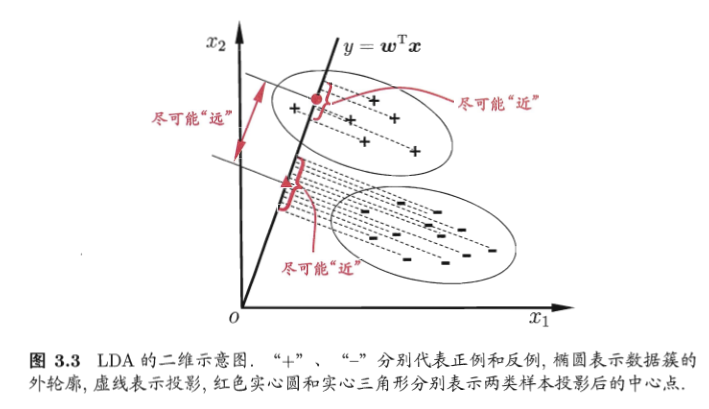

lda.png
lda.png

那什么是线性判别分析呢？所谓线性判别分析，就是将样本数据点投影到直线上，直线函数的解析式又称为线性函数，通常的表达式为：

其中$w$表示特征向量，$x$表示样本列向量，$y$表示投影后的样本列向量。
首先对两类样本进行考虑分析，然后在推广到多维问题。
给定数据集$D=^m{i=1},y∈(0,1)$，$X_i,\mu_i,\Sigma_i$分别表示$i\in{0, 1}$类示例的集合、均值向量、协方差矩阵。若将数据投影到直线$w$上，则两类样本的中心在直线上的投影分别为$ w^\mathrm T\mu_0$和 $ w^\mathrm T \mu_1$；若将所以样本点都投影到之想爱你上，则两类样本的协方差矩阵分别为$w^\mathrm T\Sigma_0w$和$w^\mathrm T\Sigma_1w$。
想要使得同类样本的投影带你尽可能地接近，可以让同类样本点的投影点的协方差尽可能的小，即$w^\mathrm T\Sigma_0w$+$w^\mathrm T\Sigma_1w$尽可能小；而若想要异类样本的投影点尽可能的远离，可以让类中心带你的距离尽可能的大，即$||w^\mathrm T\mu_0-w^\mathrm T\mu_1||$尽可能大，同时考虑即可得到待优化的目标：

定义类内散度矩阵（within-class scatter matrix）

以及类间散度矩阵（between-class scatter matrix）

所以待优化目标为

这就是LDA欲最大化的目标表达，即$ S_b $和$S_w$的“广义瑞利商”（generalized Rayleigh quotient）.
如何求取$w$呢？
对于瑞利商来说，分子分母都是关于$w$的二次项，因此其解与$w$的长度无关，只与其方向有关，所以不妨令$w^\mathrm TS_ww=1$，则有：

由拉格朗日乘子法得到等价式

其中，$\lambda$是拉格朗日乘子。注意到$S_bw$的方向为$(\mu_0-\mu_1)$，令

即可得

$w$的最大值就是矩阵$S_w^{-1}S_b$的最大特征值。
至此，投影面即可得到。

python实现以及结果展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import numpy as np
import matplotlib.pyplot as plt


# 生成两类随机样本
def createdata():
    points1 = np.mat(np.random.random((10, 2))*2+4)
    points2 = np.mat(np.random.random((10, 2))*3+2)

    return points1, points2


# 计算样本均值
def cal_mean(samples, num):
    ave = []
    a, b = np.shape(samples[num])
    for i in range(b):
        n = np.sum(samples[num][:, i]) / a
        ave.append(n)
    return np.array(ave)


# 计算类内离散度和类间离散度
def cal_swb(samples):
    # 获取样本的行列值
    a, b = np.shape(samples[0])
    # 获取样本
    points1, points2 = samples[0:2]
    # 调用求均值函数
    pointsmean1 = np.mat(cal_mean(points1, 0))
    pointsmean2 = np.mat(cal_mean(points2, 1))
    allpointsmean1 = (pointsmean1 + pointsmean2)/2
    # 先计算第一类类内离散矩阵
    s1 = 0
    for i in range(a):
        s1 = s1 + (points1[i, :] - pointsmean1).T * (points1[i, :] - pointsmean1)
    s2 = 0
    for i in range(a):
        s2 = s2 + (points2[i, :] - pointsmean2).T * (points2[i, :] - pointsmean2)
    sw = (a*s1 + a*s2)/(a + a)

    # 计算类间离散矩阵
    sb = (pointsmean1 - pointsmean2).T*(pointsmean1 - pointsmean2)
    return np.mat(sw), np.mat(sb), np.mat(allpointsmean1)


samples = createdata()
plt.plot(samples[0][:, 0], samples[0][:, 1], 'b.')
plt.plot(samples[1][:, 0], samples[1][:, 1], 'r.')
""" 测试 """
print(samples[0].shape)
pointsmean1 = cal_mean(samples, 0)
pointsmean2 = cal_mean(samples, 1)
print(pointsmean1)
print(pointsmean2)
sw, sb, allmean = cal_swb(samples)
# print(sw.shape)
# print(sb.shape)
# print(np.linalg.inv(sw))
# 求最大特征值对应的特征向量
eigvalue, eigvector = np.linalg.eig(np.linalg.inv(sw).dot(sb))
print(eigvalue)
indexvec = np.argsort(-eigvalue)
nlargestindex = indexvec[1]
print(nlargestindex)
# 最佳投影方向求得
w = np.array(eigvector[nlargestindex])
# print(w)
# print(w[0][0])
# print(w.shape)
# 绘制散点图
plt.figure()
plt.scatter(np.array(samples[0][:, 0]), np.array(samples[0][:, 1]), c='b', marker='o')
plt.scatter(np.array(samples[1][:, 0]), np.array(samples[1][:, 1]), c='r', marker='*')
x = np.linspace(0, 10, num=50)
y = w[0][1]/w[0][0]*x
x1 = np.array((samples[0][:, 0] + samples[0][:, 1]*(w[0][1]/w[0][0]))/(1+(w[0][1]/w[0][0])**2))
x2 = np.array((samples[1][:, 0] + samples[1][:, 1]*(w[0][1]/w[0][0]))/(1+(w[0][1]/w[0][0])**2))
y1 = w[0][1]/w[0][0]*x1
y2 = w[0][1]/w[0][0]*x2
plt.scatter(x1, np.array(y1), c='c', marker='o')
plt.scatter(x2, np.array(y2), c='m', marker='*')
plt.plot(x, y, color='r')
plt.show()

结果展示如下

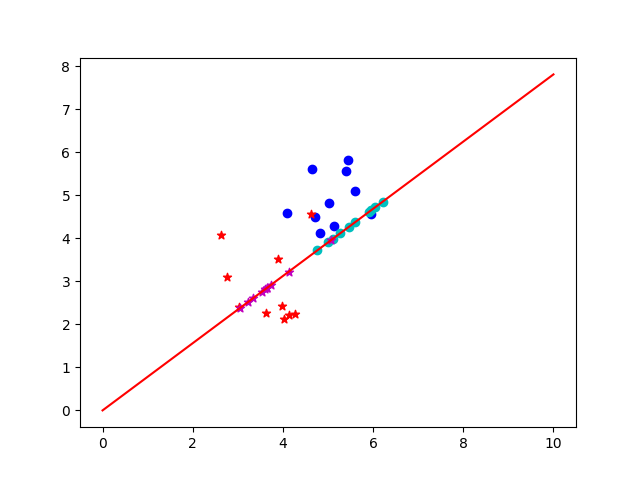
课堂小作业2（2）.png
课堂小作业2（2）.png