排序算法之选择排序

数组

数据在内存中的顺序是连续的，在使用时需要向计算机申请分配一定的内存空间，如果申请的空间一定，再加入新的数据时如果当前空间不足需要重新向计算机申请；同样，如果先前申请了大量的空间，但在使用过程中并没有被用到，则会造成空间的浪费。

术语

数组的元素带编号，编号从0开始，这个位置叫做索引，故说：”元素a位于索引1处“，在元素读取和插入时有以下特征：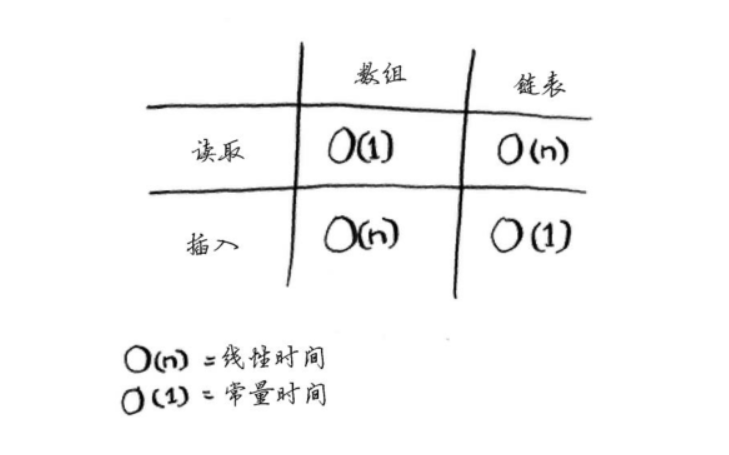

数组和链表操作.png
数组和链表操作.png

由于索引的存在，所以数组在读取数据时就有很快的速度；但在插入数据方面，需要将待插入位置的后面的所有数据向后移位，时间较长。

链表

链表中的元素可存储在内存的任何地方，其中的每个元素存放的都是下一个元素的地址，这样就能使一系列的内存地址串在一起。
删除操作时，链表是更好的选择，只需要修改前一个元素指向的地址。

选择排序

算法思想：首先在未排序的队列中选择最小或者最大的元素，并存放到新队列的起始位置；然后再从剩余的元素中选择最小或者最大的一个，再将其放入到新队列的后面，以此重复操作。

乐队歌曲作品如下：

选择排序1.png
选择排序1.png

对列表中的歌曲按照播放次数降序排列，进而将自己喜欢的音乐进行排序。方法即是遍历列表，找出播放次数最多的音乐，然后将其添加到新列表里。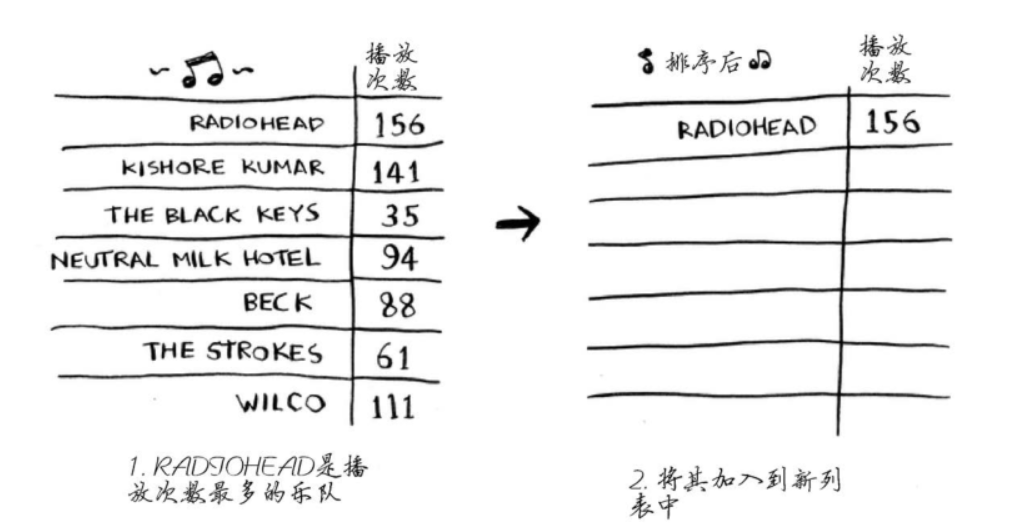
选择排序2.png
选择排序2.png

再次进行此操作，找出第二多的乐队。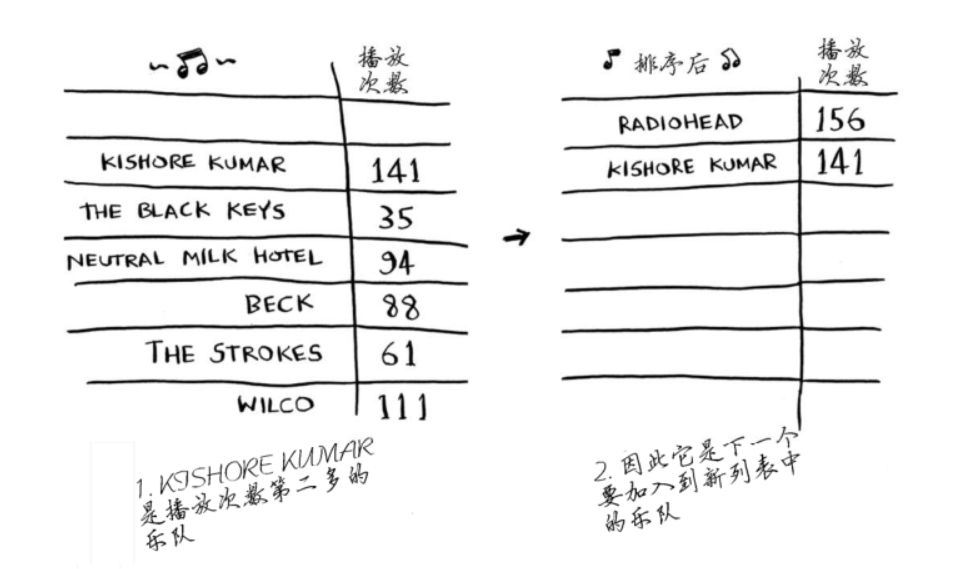
选择排序3.png
选择排序3.png

继续这样做，进而得到一个新的有序列表。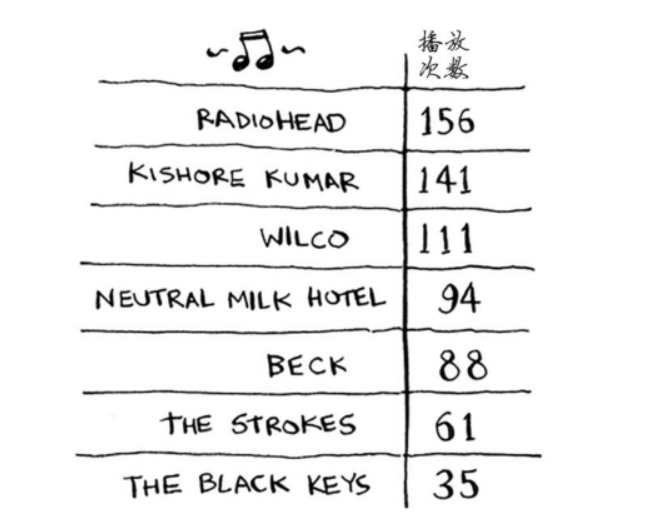
选择排序4.png
选择排序4.png

时间复杂度上来看，对于列表里的n个元素，需要对每个元素都进行查看，所以时间复杂度为O（n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def findsmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index


def selectsort(arr):
    newarr = []
    for i in range(len(arr)):
        smallest = findsmallest(arr)
        newarr.append(arr.pop(smallest))

    return newarr

print(selectsort([3, 7, 2, 1, 9, 6]))

输出结果如下：

1
[1, 2, 3, 6, 7, 9]